Exploring models for network meta-analysis with ASReml-R

Jul 2, 2025 R

Meta-analysis is a powerful method for comparing treatments across studies by summarizing and combining treatment effects. Traditionally, this involves extracting a single effect size per study—such as a difference in means, log odds ratio, or standardized response—and aggregating these across studies. This approach works well when comparing just two treatments, but what if you want to evaluate multiple treatments across many studies, where not every study includes the same treatments?

Network meta-analysis (NMA), a.k.a. multiple treatments meta-analysis, extends traditional methods by allowing simultaneous estimation and ranking of multiple treatments, even when some have never been directly compared. NMA synthesizes both direct comparisons (within studies) and indirect comparisons (via shared treatments across studies). For example, if trial A compares treatments 1 vs. 2, and trial B compares 2 vs. 3, NMA enables inference on 1 vs. 3.

This approach is especially valuable in agricultural research, where multi-environment trials are common and each site often tests only a subset of treatments. The resulting data form a network of incomplete and overlapping comparisons, far from an ideal full factorial design. Pairwise meta-analysis falls short here—it discards indirect evidence, treats contrasts separately, and ignores within-study correlations. NMA, in contrast, borrows strength across the network, using shrinkage and indirect connections to produce coherent estimates—even when the data are sparse or unbalanced.

In this post, we focus on summary-level NMA, where each treatment in a trial is represented by a mean and its associated variance or weight. This reflects the type of data typically available in published studies or trial reports, particularly in plant pathology. In a future post, we’ll explore individual plot-level data (IPD), which allows for spatial modeling, trial-specific error structures, plot-level covariates, and other interaction effects.

Whether you work in plant breeding, pathology, agronomy, or statistics, this post walks through several NMA models using ASReml-R, a commercial mixed model package in R. ASReml-R excels in modeling complex variance structures—an advantage when working with unbalanced trial data and heterogeneity across locations.

Loading Packages

We start by loading the necessary packages and importing data from Madden, Piepho, and Paul (2016). This data originates from Paul et al. (2010), who analyzed wheat yield across 136 wheat field trials over 12 years in 14 U.S. states. For details about the dataset, please, refer to the publications above. Briefly, each ach trial followed a randomized complete block design and included at least two treatments: a no-fungicide control and tebuconazole (Folicur). Other fungicides—propiconazole (Tilt), prothioconazole (Proline), tebuconazole + prothioconazole (Prosaro), and metconazole (Caramba)—were included in different combinations. Most studies evaluated four treatments on average. The authors provide data for second-stage analysis, consisting of treatment mean yields and their corresponding sampling variances. The first-stage ANOVA has already been conducted, and these summary statistics serve as the basis for the network meta-analysis presented here.

Variables from this dataset include:

trial: Numeric study ID
trt: Treatment code (10 = Control, 2 to 6 = fungicides)
yield: Mean yield per treatment in each study (the summary effect size)
varyld: Within-study sampling variance of yield (1/wtyld)
wtyld: Inverse variance weight (used in model fitting) (1/varyld)
cla: Wheat marketing class (S = soft, W = white); a potential moderator
group: Study classification based on treatment combinations (13 unique groups)

pacman::p_load(
  janitor,    # For cleaning column names
  tidyverse,  # For data wrangling and visualization
  asreml      # For fitting mixed models
)

## Online License checked out Wed Jul  2 17:16:52 2025

Importing and Preparing the Data

We now import the trial data and preprocess it by cleaning names, recoding treatments, and converting yield units. Sampling variances are also adjusted accordingly.

path = file.path("c:/Users/garnica/", "OneDrive - The Ohio State University")

dat =  read_csv(file.path(path, "madden_2016.csv"), show_col_types = FALSE) %>%
  janitor::clean_names() %>%
  mutate(across(c(trial, trt, cla, group), as_factor)) %>%
  mutate(trt = fct_recode(trt,
    "Teb"   = "2",  # Tebuconazole (Folicur)
    "Prop"  = "3",  # Propioconazole
    "Prothi"= "4",  # Prothioconazole
    "ProTe"  = "5",  # Proth. + Tebu. (Prosaro)
    "Metc"  = "6",  # Metconazole (Caramba)
    "Chk"   = "10"  # Control
  ),
  yield  = yield * 0.0628,
  varyld = varyld * (0.0628^2),
  wtyld = 1/varyld)

trt_levels = levels(dat$trt)
n_trt = length(trt_levels)

The fungicide treatments tested include:

Teb: Tebuconazole
Propi: Propioconazole
Propi: Prothioconazole
Prothi: Prothioconazole
ProTe: Proth.+Tebu
Met: Metconazole
Ckc: Control

Fitting the Network Meta-Analysis Models

We now fit a series of NMA models using ASReml-R, ranging from simple fixed-effect models to those with random treatment-by-study interactions. Each model offers a different approach to handling heterogeneity and network structure. ASReml-R fits models using restricted maximum likelihood (REML).

For a detailed description of the model formulations, their theoretical foundations, and corresponding SAS code implementations, readers are encouraged to consult the original paper by Madden, Piepho, and Paul (2016). Throughout this blog, I refer to that publication simply as the original manuscript. We also don’t replicate their entire study, only models below.

Model F1: Fixed Study and Treatment Effects, Homogeneous Treatment Effects

This model corresponds to Equation 5 in the original manuscript. It includes fixed effects for treatment and trial, and a random trial-by-treatment interaction to account for study-specific deviations.

mod.f1 = asreml(
  fixed = yield ~ trt + trial,                   # fixed terms 
  random = ~ trial:trt,                          # random terms 
  weights = "wtyld",                             # inverse of sampling variance
  data = dat,
  family = asr_gaussian(dispersion = 1),         # term holds the residual variance at 1 
  na.action = na.method(x = "omit",y = "omit"),  # omit NAs
  trace=FALSE                                    # quiet
  )

Variance Component Estimates

summary(mod.f1)$varcomp

##           component   std.error  z.ratio bound %ch
## trial:trt 0.0252785 0.003186639 7.932652     P   0
## units!R   1.0000000          NA       NA     F   0

The estimated variance for the trial × treatment interaction $({\hat{σ}}_{u})$ is approximately 0.025, indicating moderate heterogeneity in treatment performance across trials. This is the same value as reported in the original manuscript and independent SAS analyses I conducted using their code.

Wald Test for Fixed Effects

wald(mod.f1)

## [0;34mWald tests for fixed effects.[0m
## [0;34mResponse: yield[0m
## [0;34mTerms added sequentially; adjusted for those above.[0m
## 
##                Df Sum of Sq Wald statistic Pr(Chisq)    
## (Intercept)     1    167025         167025 < 2.2e-16 ***
## trt             5       619            619 < 2.2e-16 ***
## trial         135     17292          17292 < 2.2e-16 ***
## residual (MS)             1                             
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

All fixed effects (treatment, trial) are highly significant (p < 0.001), so detailed tables thereafter are omitted for brevity.

Treatment Predictions and Standard Errors

predict(mod.f1,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)

## $pvals
## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The simple averaging set: trial
## [0m
##      trt predicted.value  std.error    status
## 1    Teb        3.809541 0.01271891 Estimable
## 2   Prop        3.733358 0.02835202 Estimable
## 3 Prothi        3.962010 0.02870707 Estimable
## 4  ProTe        3.966686 0.02071686 Estimable
## 5   Metc        3.969842 0.02108578 Estimable
## 6    Chk        3.535234 0.01271891 Estimable
## 
## $avsed
##        min       mean        max 
## 0.01734277 0.02959465 0.04025298 
## 
## $vcov
## 6 x 6 Matrix of class "dspMatrix"
##              [,1]         [,2]         [,3]         [,4]         [,5]
## [1,] 1.617708e-04 6.773186e-06 4.562688e-06 7.216585e-06 5.934918e-06
## [2,] 6.773186e-06 8.038370e-04 3.815346e-06 1.636593e-05 2.456773e-05
## [3,] 4.562688e-06 3.815346e-06 8.240962e-04 5.438039e-05 3.340547e-05
## [4,] 7.216585e-06 1.636593e-05 5.438039e-05 4.291881e-04 5.754458e-05
## [5,] 5.934918e-06 2.456773e-05 3.340547e-05 5.754458e-05 4.446103e-04
## [6,] 1.138491e-05 6.773186e-06 4.562688e-06 7.216585e-06 5.934918e-06
##              [,6]
## [1,] 1.138491e-05
## [2,] 6.773186e-06
## [3,] 4.562688e-06
## [4,] 7.216585e-06
## [5,] 5.934918e-06
## [6,] 1.617708e-04
## 
## $sed
## 6 x 6 Matrix of class "dspMatrix"
##            [,1]       [,2]       [,3]       [,4]       [,5]       [,6]
## [1,]         NA 0.03085549 0.03125287 0.02401095 0.02438260 0.01734277
## [2,] 0.03085549         NA 0.04025298 0.03464525 0.03463108 0.03085549
## [3,] 0.03125287 0.04025298         NA 0.03383081 0.03466837 0.03125287
## [4,] 0.02401095 0.03464525 0.03383081         NA 0.02754468 0.02401095
## [5,] 0.02438260 0.03463108 0.03466837 0.02754468         NA 0.02438260
## [6,] 0.01734277 0.03085549 0.03125287 0.02401095 0.02438260         NA

This output includes:

pvals: Predicted yield per treatment and associated standard errors. For instance, the estimate for “Teb” is ~3.8095 t/ha with SE = 0.0127.

avsed: Summary statistics of the average standard errors of differences (SEDs) between treatment means, including minimum, mean, and maximum values. This gives a sense of the precision when comparing treatments.

vcov: The variance-covariance matrix of treatment effect estimates, with variances on the diagonal and covariances off-diagonal. This matrix is useful for constructing confidence intervals and performing contrasts between treatments.

sed: The matrix of standard errors of differences between pairs of treatment means. These values represent the uncertainty in direct comparisons between treatments, accounting for their covariance.

This model reproduces the predicted treatment means reported in the original manuscript—for example, “Fol” has an estimated yield of 3.8101 t/ha—but yields slightly smaller standard errors (e.g., SE = 0.01777), likely due to differences in small model mispecifications or estimation methods.

Model F2: Separate Between-Study Variances per Treatment

Model F2 generalizes Model F1 by allowing each treatment to have its own between-study variance. While the study effect remains fixed, the treatment-by-trial interaction is modeled with a diagonal variance structure. This results in treatment-specific heterogeneity so that each treatment has its own variance component $({\hat{σ}}_{u (j)})$ for the jth fungicide treatment.

mod.f2 = asreml(
  fixed = yield ~ trial + trt,
  random = ~ diag(trt):trial,                         # diagonal
  weights = "wtyld",
  data = dat,
  na.action = na.method(x = "omit",y = "omit"),
  family = asr_gaussian(dispersion = 1),
  maxiter = 100,
  trace = FALSE
)

mod.f2 = update.asreml(mod.f2)                        # convergence

Convergence was achieved by updating the model at least once. Madden, Piepho, and Paul (2016) suggested exploring different starting values for the nonresidual variance parameters in order to achieve convergence.

Variance Component Estimates

summary(mod.f2)$varcomp

##                         component   std.error   z.ratio bound %ch
## trt:trial!trt_Teb    2.114030e-02 0.006998125 3.0208524     P 0.0
## trt:trial!trt_Prop   2.411802e-02 0.010655591 2.2634149     P 0.0
## trt:trial!trt_Prothi 6.295539e-08          NA        NA     B  NA
## trt:trial!trt_ProTe  1.831266e-02 0.007180796 2.5502268     P 0.0
## trt:trial!trt_Metc   1.598393e-03 0.004718162 0.3387746     P 0.2
## trt:trial!trt_Chk    6.203336e-02 0.011744841 5.2817536     P 0.0
## units!R              1.000000e+00          NA        NA     F 0.0

The estimated variance components represent the magnitude of between-study heterogeneity for each treatment (on the yield scale, t²/ha²). Values range from near zero—such as for Prothi $({\hat{σ}}_{u (P r o t h i)}^{2})$ to moderate such as Chk $({\hat{σ}}_{u (C h k)}^{2})$ at 0.062 and Teb $({\hat{σ}}_{u (F o l)}^{2})$ at 0.021. The control shows the greatest variability across trials, while other fungicides exhibit moderate and statistically significant heterogeneity. These findings indicate that treatments differ not only in average yield performance but also in their stability across environments.

Treatment Predictions and Standard Errors

predict(mod.f2,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)$pvals

## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The simple averaging set: trial
## [0m
##      trt predicted.value  std.error    status
## 1    Teb        3.810066 0.01266783 Estimable
## 2   Prop        3.740635 0.02792308 Estimable
## 3 Prothi        3.952945 0.02247956 Estimable
## 4  ProTe        3.968788 0.01992606 Estimable
## 5   Metc        3.977343 0.01781478 Estimable
## 6    Chk        3.536230 0.01300835 Estimable

Predicted values are nearly identical across models, with changes <0.01 t/ha. Standard errors generally decreased in Model F2, especially for treatments with lower estimated between-study variance (e.g., Met, Prothi).

Comparing Model F1 and Model F2

mods.asr = list(mod.f1,mod.f2)
asremlPlus::infoCriteria(mods.asr)

##   fixedDF varDF NBound       AIC       BIC   loglik
## 1       0     1      1 -615.9944 -611.9613 308.9972
## 2       0     5      2 -637.0881 -616.9227 323.5440

Model F2 has a smaller AIC (−637.0881) and is therefore preferred when comparing models with the same fixed effects. However, AIC-based comparison is invalid for models that differ in their fixed-effects structure.

Model R1: Random study effects, homogeneity of treatment effects

In this modification, Model F1 incorporates a random effect for study, analogous to a linear mixed model for incomplete block designs with random blocks. This structure enables the model to borrow information on treatment effects both within studies (intrastudy) and between studies (interstudy), improving the estimation by combining these sources of variation.

mod.r1 = asreml(
  fixed = yield ~ trt,           
  random = ~ trial + trt:trial,   
  weights = "wtyld",             
  data = dat,
  family = asr_gaussian(dispersion = 1),  
  maxiter = 100,
  na.action = na.method(x = "omit",y = "omit"),
  initial = list(                                                 # starting values
    list(factor = "trial", component = 1),   
    list(factor = "trt:trial", component = 1),  
    list(factor = "units", component = 1)),
  boundary = list(
    list(factor = "units", component = "F")),
  trace = FALSE
  )

Variance Component Estimates

sum.r1 = summary(mod.r1)$varcomp;sum.r1

##            component   std.error  z.ratio bound %ch
## trial     1.53821098 0.188845454 8.145343     P   0
## trt:trial 0.02528862 0.003187579 7.933489     P   0
## units!R   1.00000000          NA       NA     F   0

The random statement specifies the variance-covariance structure of the vvector, which includes both the random study effect and the study-by-treatment interaction. This defines the . Under the compound symmetry (CS) specification, the variance component $({\hat{σ}}_{β})$ represents the covariance between treatment effects within a study, and is therefore allowed to take negative values—though in practice, it is typically estimated as nonnegative. This model includes three random-effect parameters:

The between-study variance (for study main effects) ${\hat{σ}}_{β}^{2}$
The treatment-by-study interaction variance ${\hat{σ}}_{u}^{2}$
The within-study residual variance (set at 1)

G matrix

var_beta = sum.r1["trial", "component"]
var_u    = sum.r1["trt:trial", "component"]
I_mat = diag(n_trt)
J_mat = matrix(1, n_trt, n_trt)
G = var_beta * J_mat + var_u * I_mat
rownames(G) = colnames(G) = trt_levels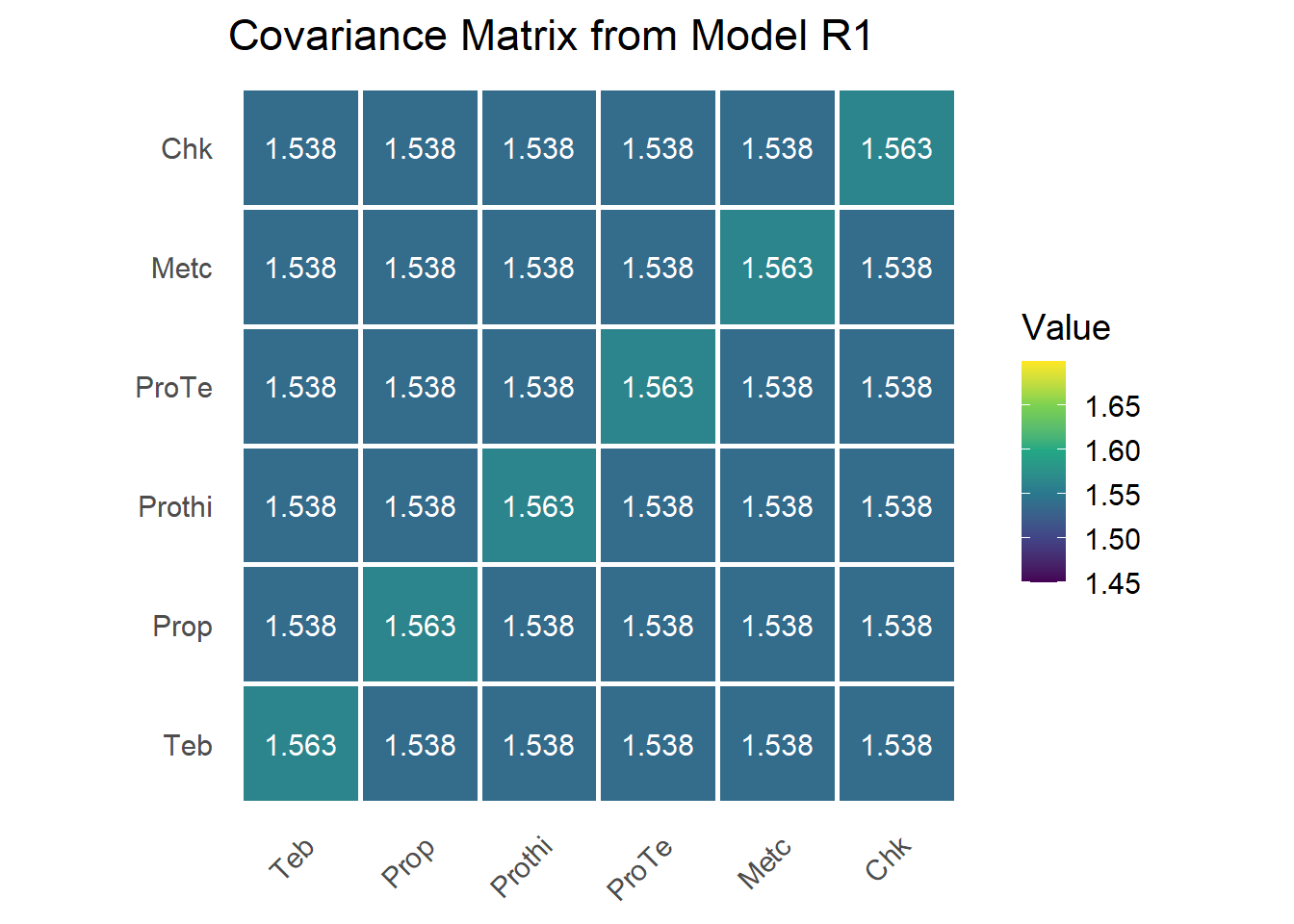

Under the CS covariance structure, the estimated $G$ matrix for treatment effects has:

Equal variances along the diagonal: $Var (h_{i j}) = {\hat{σ}}_{β}^{2} + {\hat{σ}}_{u}^{2}$

Equal covariances off-diagonal: $Cov (h_{i j}, h_{i k}) = {\hat{σ}}_{β}^{2}$

This implies all treatment effects within a trial share a common correlation, and the variability across trials is decomposed into:

${\hat{σ}}_{β}^{2}$ : Shared between-treatment covariance within trials

${\hat{σ}}_{u}^{2}$ : Treatment-specific deviations within trials

This structure reflects constant variance across treatments and equal covariance between treatment effects within studies, a hallmark of the CS assumption.

Treatment Predictions and Standard Errors

predict(mod.r1,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)$pvals

## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The ignored set: trial
## [0m
##      trt predicted.value std.error    status
## 1    Teb        3.807871 0.1079718 Estimable
## 2   Prop        3.732877 0.1108996 Estimable
## 3 Prothi        3.962304 0.1109909 Estimable
## 4  ProTe        3.966229 0.1092001 Estimable
## 5   Metc        3.969550 0.1092708 Estimable
## 6    Chk        3.533565 0.1079718 Estimable

This gives the exact results of SAS.

Model R2: Heterogeneous Compound Symmetry (CSH)

Model R2 extends the compound symmetry structure (Model R1) by allowing treatment-specific variances while maintaining a common correlation among treatments within studies. This is known as the heterogeneous compound symmetry (CSH) structure. It is implemented using corh(trt):trial, which specifies a diagonal variance-covariance structure with a shared correlation parameter.

mod.r2 = asreml(
  fixed = yield ~ trt,
  random = ~ corh(trt):trial,                        # heterogeneous compound symmetry
  weights = "wtyld",
  data = dat,
  family = asr_gaussian(dispersion = 1),
  maxiter = 200,
  na.action = na.method(x = "omit",y = "omit"),
  trace = FALSE
)

Variance Component Estimates

sum.r2 = summary(mod.r2)$varcomp;sum.r2

##                      component   std.error    z.ratio bound %ch
## trt:trial!trt!cor    0.9845368 0.002722035 361.691418     U 0.0
## trt:trial!trt_Teb    1.5430249 0.190560378   8.097302     P 0.0
## trt:trial!trt_Prop   1.5353600 0.200817634   7.645544     P 0.0
## trt:trial!trt_Prothi 1.5423652 0.204580818   7.539148     P 0.1
## trt:trial!trt_ProTe  1.5165437 0.192193973   7.890693     P 0.1
## trt:trial!trt_Metc   1.4375120 0.183292329   7.842729     P 0.1
## trt:trial!trt_Chk    1.6763460 0.207330726   8.085372     P 0.0
## units!R              1.0000000          NA         NA     F 0.0

With six treatments, the model estimates six treatment-specific variances for fungicide treatments (labelled trt:trial!trt_), one correlation parameter (labeled !cor), representing the shared correlation $\hat{ρ}$ between treatment effects within studies, one residual (within-study) variance, typically fixed at 1 for weighted meta-analysis. This model generalizes the equal-variance assumption of CS by letting each treatment have a unique total variance while still sharing a common correlation structure.

G matrix

variances = sum.r2[!grepl("(cor|R)$", rownames(sum.r2)), 1]
rho = sum.r2[grepl("cor$", rownames(sum.r2)), 1]
G = diag(1, n_trt)
G[upper.tri(G)] = rho
G[lower.tri(G)] = t(G)[lower.tri(G)]
G = diag(sqrt(variances)) %*% G %*% diag(sqrt(variances))
rownames(G) = colnames(G) = trt_levels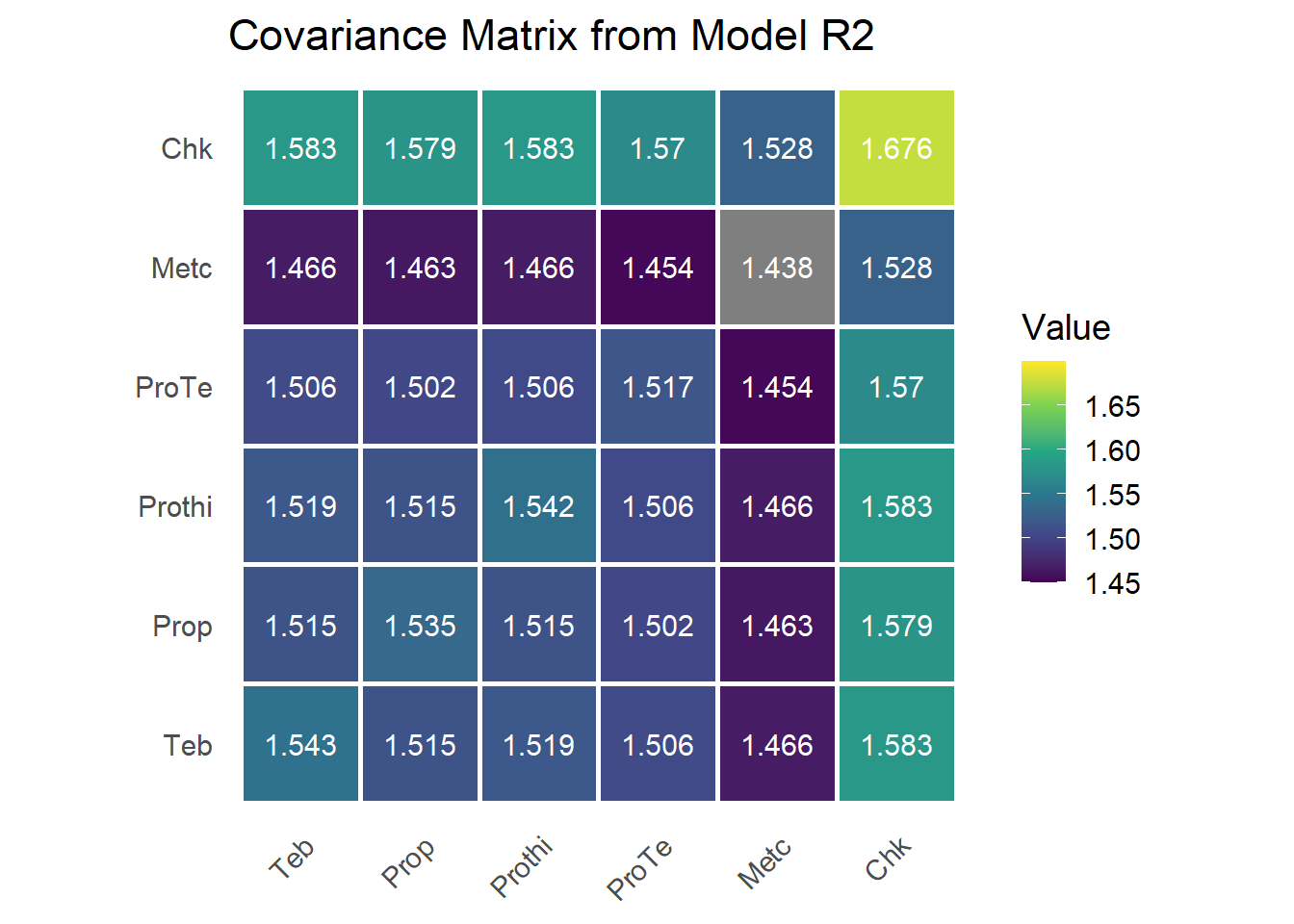

More parameters estimated in the $G$ matrix for treatment effects.

Treatment Predictions and Standard Errors

predict(mod.r2,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)$pvals

## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The ignored set: trial
## [0m
##      trt predicted.value std.error    status
## 1    Teb        3.806563 0.1072693 Estimable
## 2   Prop        3.732439 0.1098536 Estimable
## 3 Prothi        3.964428 0.1102102 Estimable
## 4  ProTe        3.966996 0.1075672 Estimable
## 5   Metc        3.971398 0.1048453 Estimable
## 6    Chk        3.537911 0.1117421 Estimable

Exact values of SAS output.

Model R3: Unstructured (UN)

Model R3 specifies an unstructured (UN) variance-covariance matrix for treatment effects across studies. This is the most flexible structure, allowing each treatment to have its own variance and each pair of treatments its own covariance. It is implemented in ASReml-R using us(trt):trial.

mod.r3 = asreml(
  fixed = yield ~ trt,
  random = ~ us(trt):trial,                           # unstructured 
  weights = "wtyld",
  data = dat,
  family = asr_gaussian(dispersion = 1),  
  workspace = "8gb",
  pworkspace = "8gb",
  maxiter = 200,
  initial = list(
    list(factor = "units", component = 1)),
  boundary = list(
    list(factor = "units", component = "F")),
  na.action = na.method(x = "omit",y = "omit"),
  trace = FALSE
)

This model is not fitting particularly well but we report it here anyways. I could give better start values but for brevity, let’s keep it that way. #### Variance Component Estimates

sum.r3 = summary(mod.r3)$varcomp;sum.r3

##                             component std.error  z.ratio bound %ch
## trt:trial!trt_Teb:Teb        1.534306 0.1894097 8.100462     ?   0
## trt:trial!trt_Prop:Teb       1.522741 0.1897810 8.023675     ?   0
## trt:trial!trt_Prop:Prop      1.540264 0.1983273 7.766275     ?   0
## trt:trial!trt_Prothi:Teb     1.511731 0.1892805 7.986722     ?   0
## trt:trial!trt_Prothi:Prop    1.512296 0.1919247 7.879632     ?   0
## trt:trial!trt_Prothi:Prothi  1.528557 0.1989125 7.684569     ?   0
## trt:trial!trt_ProTe:Teb      1.514811 0.1880826 8.053966     ?   0
## trt:trial!trt_ProTe:Prop     1.503409 0.1897361 7.923683     ?   0
## trt:trial!trt_ProTe:Prothi   1.525400 0.1919188 7.948153     ?   0
## trt:trial!trt_ProTe:ProTe    1.533243 0.1937043 7.915382     ?   0
## trt:trial!trt_Metc:Teb       1.472531 0.1826996 8.059849     ?   0
## trt:trial!trt_Metc:Prop      1.476626 0.1854131 7.963982     ?   0
## trt:trial!trt_Metc:Prothi    1.485992 0.1862277 7.979433     ?   0
## trt:trial!trt_Metc:ProTe     1.480930 0.1854579 7.985261     ?   0
## trt:trial!trt_Metc:Metc      1.446375 0.1828702 7.909299     ?   0
## trt:trial!trt_Chk:Teb        1.580486 0.1952290 8.095546     ?   0
## trt:trial!trt_Chk:Prop       1.587571 0.1979958 8.018206     ?   0
## trt:trial!trt_Chk:Prothi     1.556227 0.1963953 7.923952     ?   0
## trt:trial!trt_Chk:ProTe      1.540360 0.1938838 7.944755     ?   0
## trt:trial!trt_Chk:Metc       1.518974 0.1897472 8.005252     ?   0
## trt:trial!trt_Chk:Chk        1.674339 0.2065607 8.105798     ?   0
## units!R                      1.000000        NA       NA     F   0

With six treatments, the unstructured model estimates 6 treatment-specific variances, 15 treatment-by-treatment covariances, 1 fixed within-study residual variance, for a total of 22 parameters. This model is the most saturated and imposes no assumptions on the structure of the $G$ matrix.

G matrix

G = matrix(0, nlevels(dat$trt), nlevels(dat$trt))
G[upper.tri(G, diag = T)] = sum.r3[grep('trt',rownames(sum.r3)),1]
G[lower.tri(G, diag = F)] = t(G)[lower.tri(t(G), diag = F)]
rownames(G) = colnames(G) = trt_levels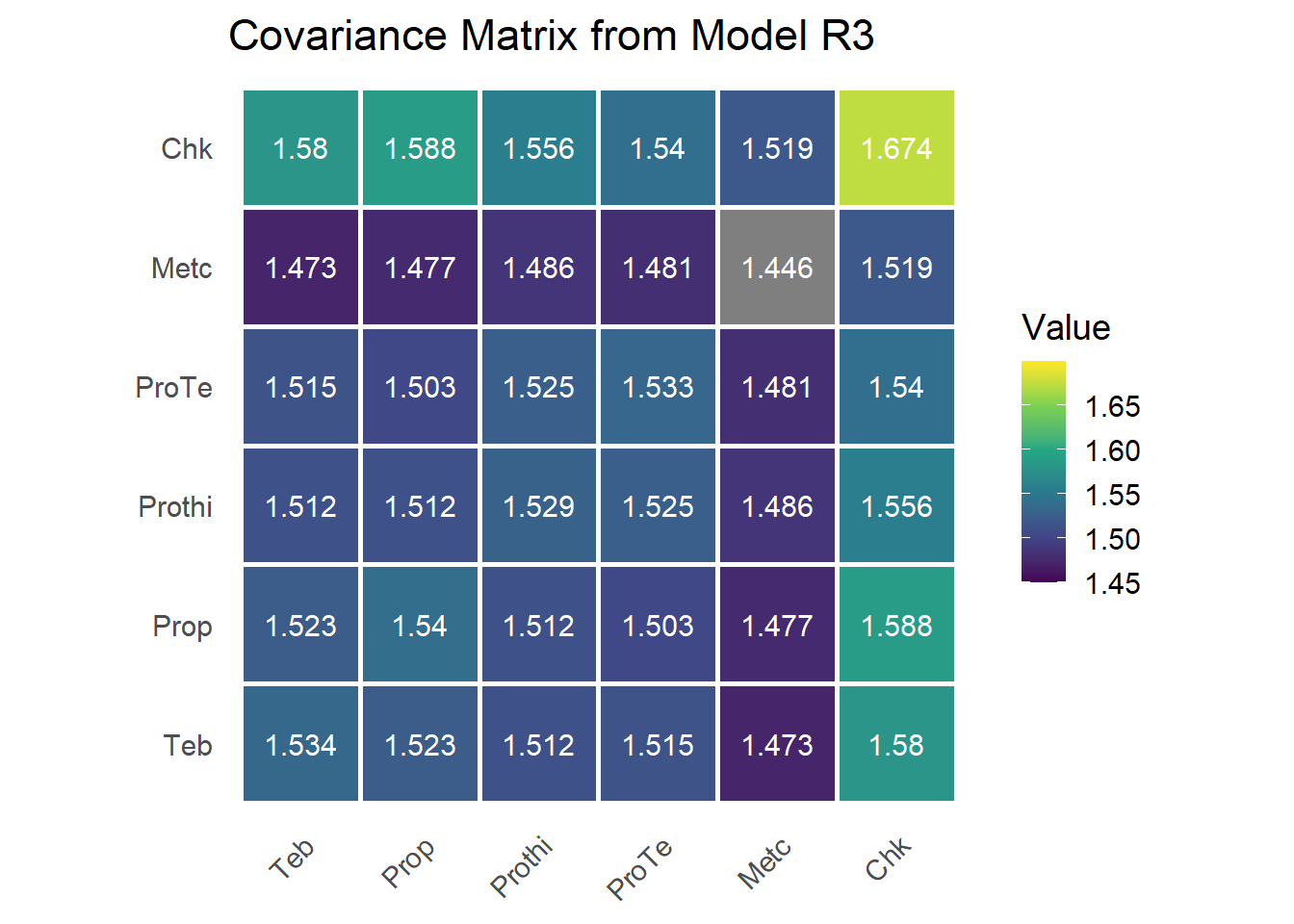

This model is the most saturated and imposes no assumptions on the structure of the $G$ matrix. The resulting $G$ matrix closely matches the SAS output from the original manuscript.

Treatment Predictions and Standard Errors

predict(mod.r3,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)$pvals

## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The ignored set: trial
## [0m
##      trt predicted.value std.error    status
## 1    Teb        3.807709 0.1069376 Estimable
## 2   Prop        3.734433 0.1093401 Estimable
## 3 Prothi        3.954665 0.1087669 Estimable
## 4  ProTe        3.979865 0.1080312 Estimable
## 5   Metc        3.985428 0.1048556 Estimable
## 6    Chk        3.535294 0.1116977 Estimable

Model R3 yields treatment means and standard errors that are very similar to those reported in the SAS-based analysis by Madden, Piepho, and Paul (2016), though minor numerical differences may occur due to implementation details.

Model R4: First-Order Factor Analytic (FA1)

The simple compound symmetry structure used in Models R1 and R2 may underfit the data, while the unstructured model (R3) may overfit by estimating too many parameters. Model R4 provides a middle ground using a first-order factor analytic (FA1) structure, which introduces a low-rank multiplicative decomposition of the variance-covariance matrix. This reduces the number of parameters while allowing flexible covariance among treatments across studies. See mathematical details in Madden, Piepho, and Paul (2016) and references therein.

mod.r4= asreml(
  fixed = yield ~ trt,
  random = ~fa(trt,1):trial,                            # FA1
  weights = "wtyld",
  family = asr_gaussian(dispersion = 1),  
  data = dat,
  na.action = na.method(x = "omit",y = "omit"),
  trace = FALSE
)
mod.r4 = update.asreml(mod.r4)                          # for convergence

Variance Component Estimates

sum.r4 = summary(mod.r4)$varcomp;sum.r4

##                                component   std.error    z.ratio bound %ch
## fa(trt, 1):trial!Teb!var    0.0207548352 0.006873266  3.0196468     P 0.0
## fa(trt, 1):trial!Prop!var   0.0234862880 0.010488704  2.2391983     P 0.0
## fa(trt, 1):trial!Prothi!var 0.0000000000          NA         NA     F  NA
## fa(trt, 1):trial!ProTe!var  0.0190030725 0.007254219  2.6195889     P 0.0
## fa(trt, 1):trial!Metc!var   0.0007039761 0.004456451  0.1579679     P 0.2
## fa(trt, 1):trial!Chk!var    0.0596499879 0.011548082  5.1653588     P 0.0
## fa(trt, 1):trial!Teb!fa1    1.2332963032 0.046228189 26.6784473     P 0.0
## fa(trt, 1):trial!Prop!fa1   1.2330378152 0.051543851 23.9221128     P 0.0
## fa(trt, 1):trial!Prothi!fa1 1.2452534274 0.047978718 25.9542871     P 0.0
## fa(trt, 1):trial!ProTe!fa1  1.2266131970 0.046834781 26.1902195     P 0.0
## fa(trt, 1):trial!Metc!fa1   1.2045659773 0.043815007 27.4920871     P 0.0
## fa(trt, 1):trial!Chk!fa1    1.2669038461 0.048731935 25.9974049     P 0.0
## units!R                     1.0000000000          NA         NA     F 0.0

With six treatments, this model estimates:

6 factor loadings (labelled !fa1)
6 treatment-specific uniqueness variances (labelled !var)
1 residual variance (held constant at 1)

This results in 7 free parameters in the $G$ , the same as in the model R2.

G matrix

fa1.loadings = sum.r4[endsWith(rownames(sum.r4),'fa1'),1]
mat.loadings = as.matrix(cbind(fa1.loadings))
svd.mat.loadings=svd(mat.loadings) 
mat.loadings.star = mat.loadings%*%svd.mat.loadings$v *-1
colnames(mat.loadings.star) = c("fa1")
psi = as.matrix(diag(sum.r4[endsWith(rownames(sum.r4),'var'),1])) 
lamb_lamb_t = mat.loadings.star %*% t(mat.loadings.star)
G = lamb_lamb_t + psi
rownames(G) = colnames(G) = trt_levels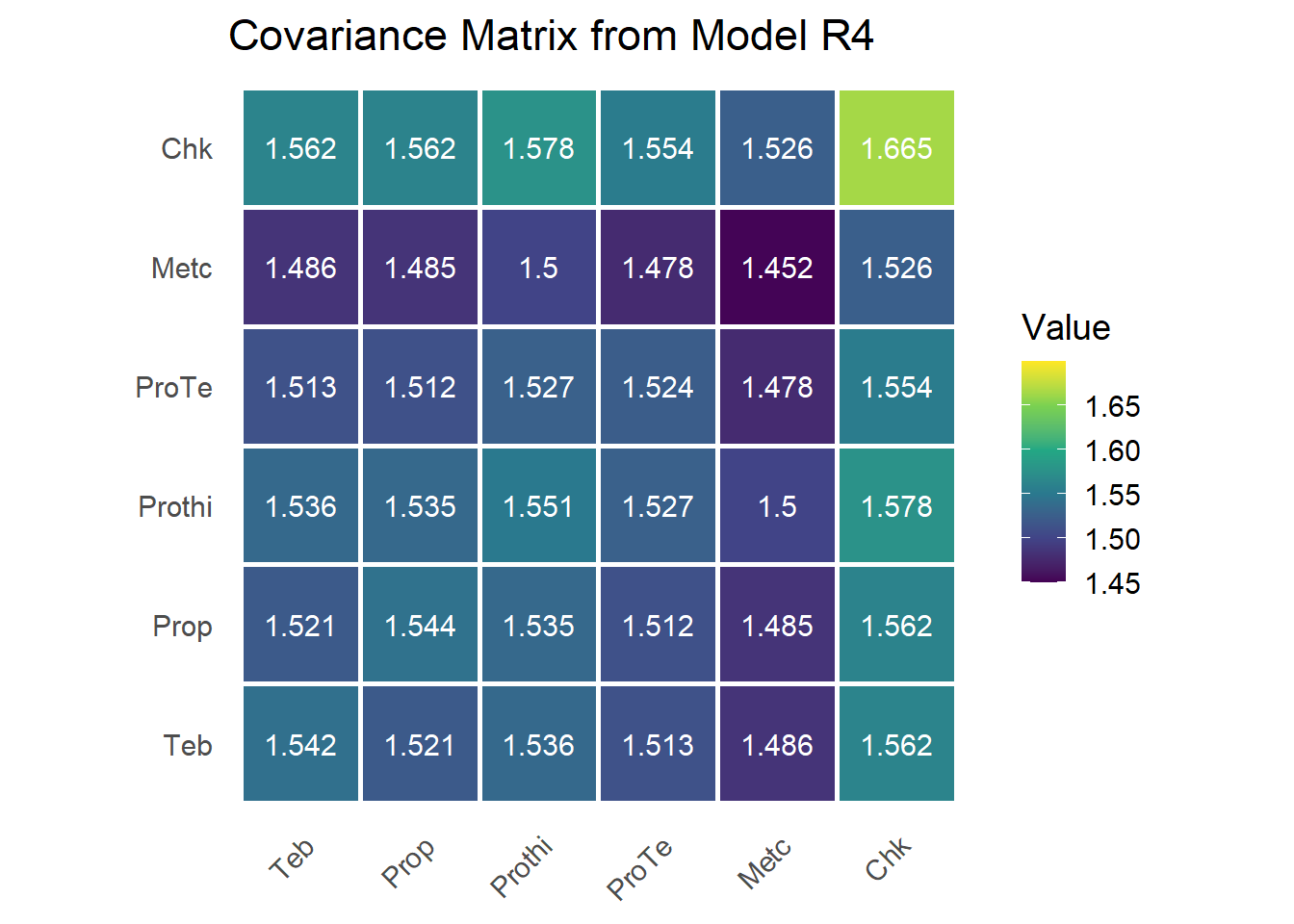

This matrix captures treatment-specific variances and their covariances via a single latent factor. Diagonal entries represent total variances, and off-diagonals represent implied covariances from shared loading on the latent dimension.

Treatment Predictions and Standard Errors

predict(mod.r4,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)$pvals

## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The ignored set: trial
## [0m
##      trt predicted.value std.error    status
## 1    Teb        3.807798 0.1072221 Estimable
## 2   Prop        3.738126 0.1100908 Estimable
## 3 Prothi        3.955384 0.1091113 Estimable
## 4  ProTe        3.968101 0.1077004 Estimable
## 5   Metc        3.976248 0.1047761 Estimable
## 6    Chk        3.537135 0.1113974 Estimable

Model R4 yields treatment means and standard errors that are very similar to those reported in the SAS-based analysis but not exactly the same.

Model R5: Second-Order Factor Analytic (FA2)

Model R5 extends FA1 by introducing a second latent dimension, allowing a richer covariance structure while using fewer parameters than the unstructured model. This approach captures more nuanced patterns of between-study variability while remaining more parsimonious than the fully unstructured model (R3).

mod.r5= asreml(
  fixed = yield ~ trt,
  random = ~fa(trt,2):trial,                         # FA2
  weights = "wtyld",
  family = asr_gaussian(dispersion = 1),  
  data = dat,
  na.action = na.method(x = "omit",y = "omit"),
  trace = FALSE
)
mod.r5 = update.asreml(mod.r5)

Variance Component Estimates

sum.r5 = summary(mod.r5)$varcomp;sum.r5

##                                component   std.error     z.ratio bound %ch
## fa(trt, 2):trial!Teb!var     0.014399874 0.006010463  2.39580125     P 0.0
## fa(trt, 2):trial!Prop!var    0.016230275 0.009689873  1.67497299     P 0.0
## fa(trt, 2):trial!Prothi!var  0.000000000          NA          NA     F  NA
## fa(trt, 2):trial!ProTe!var   0.002392005 0.006897990  0.34676841     P 0.1
## fa(trt, 2):trial!Metc!var    0.003520861 0.004823905  0.72987784     P 0.0
## fa(trt, 2):trial!Chk!var     0.001379270 0.018634047  0.07401879     P 0.3
## fa(trt, 2):trial!Teb!fa1     1.232504238 0.044682184 27.58379550     P 0.0
## fa(trt, 2):trial!Prop!fa1    1.231837776 0.049159336 25.05806385     P 0.0
## fa(trt, 2):trial!Prothi!fa1  1.231338324 0.048496738 25.39012657     P 0.0
## fa(trt, 2):trial!ProTe!fa1   1.222544093 0.046465109 26.31101310     P 0.0
## fa(trt, 2):trial!Metc!fa1    1.199053872 0.043428716 27.60970128     P 0.0
## fa(trt, 2):trial!Chk!fa1     1.281841986 0.047645386 26.90380122     P 0.0
## fa(trt, 2):trial!Teb!fa2     0.000000000          NA          NA     F  NA
## fa(trt, 2):trial!Prop!fa2   -0.036711225 0.038797431 -0.94622825     P 0.0
## fa(trt, 2):trial!Prothi!fa2  0.124818197 0.032007732  3.89962646     P 0.0
## fa(trt, 2):trial!ProTe!fa2   0.173896889 0.034970328  4.97269820     P 0.0
## fa(trt, 2):trial!Metc!fa2    0.090695242 0.027525003  3.29501299     P 0.0
## fa(trt, 2):trial!Chk!fa2    -0.172290953 0.047570273 -3.62181973     P 0.0
## units!R                      1.000000000          NA          NA     F 0.0

length(sum.r5$component)

## [1] 19

With six treatments, this model estimates:

6 first-order factor loadings (labelled !fa1)
6 second-order factor loadings (labelled !fa2)
6 treatment-specific uniqueness variances (labelled !var)
1 residual variance (fixed)

This totals 19 parameters, slightly fewer than the 22 in the unstructured model but offering a balance between flexibility and parsimony. The second latent dimension helps capture additional patterns in treatment-by-trial interaction that may not be explained by a single factor alone.

G matrix

fa1.loadings = sum.r5[endsWith(rownames(sum.r5),'fa1'),1]
fa2.loadings = sum.r5[endsWith(rownames(sum.r5),'fa2'),1]
mat.loadings = as.matrix(cbind(fa1.loadings,fa2.loadings))
svd.mat.loadings=svd(mat.loadings) 
mat.loadings.star = mat.loadings%*%svd.mat.loadings$v *-1
colnames(mat.loadings.star) = c("fa1",'fa2')
psi = as.matrix(diag(sum.r5[endsWith(rownames(sum.r5),'var'),1])) 
lamb_lamb_t = mat.loadings.star %*% t(mat.loadings.star)
G = lamb_lamb_t + psi
rownames(G) = colnames(G) = trt_levels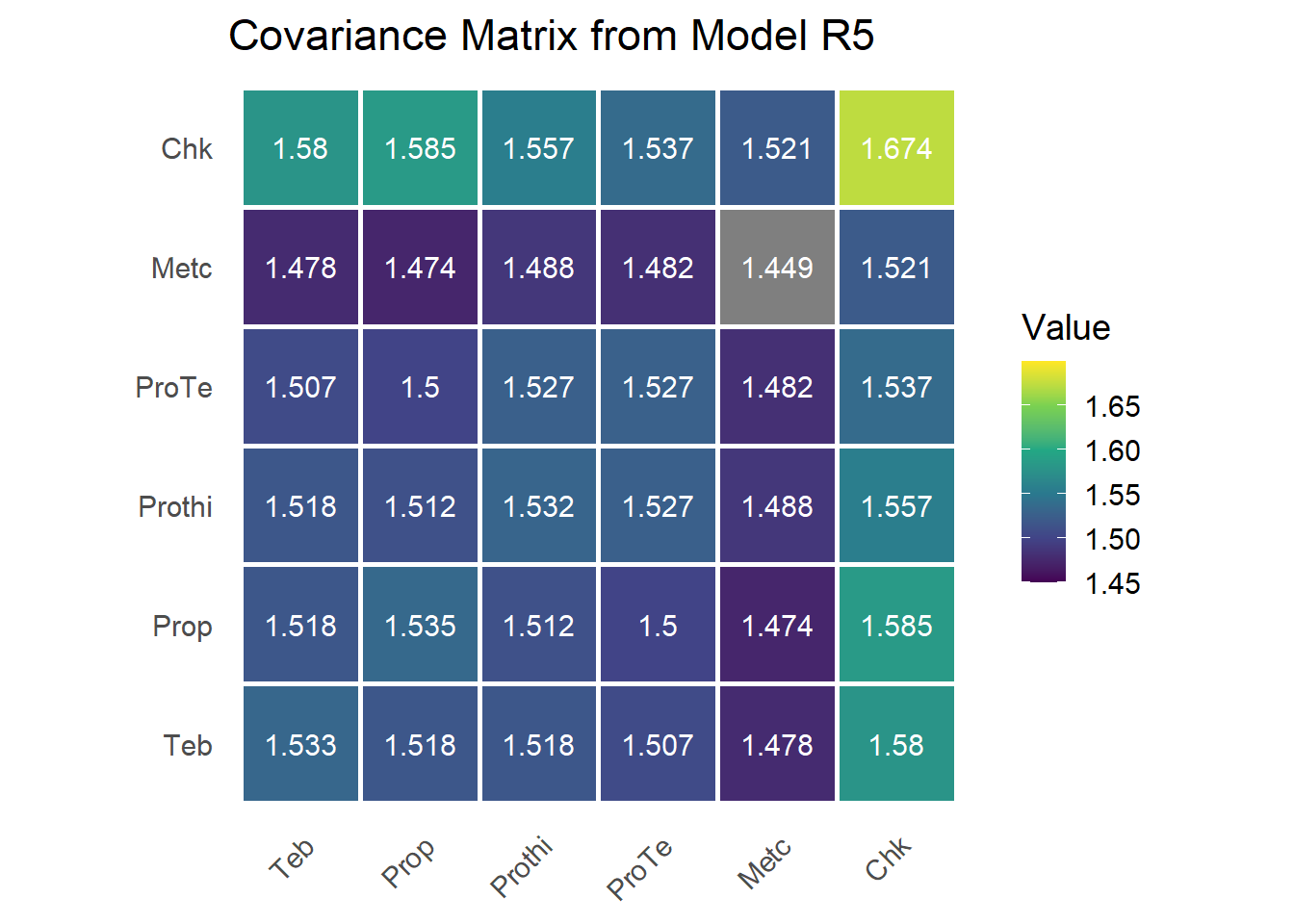

Treatment Predictions and Standard Errors

predict(mod.r5,classify = "trt", sed = TRUE, vcov = TRUE,trace=FALSE)$pvals

## 
## Notes:
## [0;34m- The predictions are obtained by averaging across the hypertable
##   calculated from model terms constructed solely from factors in
##   the averaging and classify sets.
## - Use 'average' to move ignored factors into the averaging set.
## - The ignored set: trial
## [0m
##      trt predicted.value std.error    status
## 1    Teb        3.807799 0.1069134 Estimable
## 2   Prop        3.731821 0.1092218 Estimable
## 3 Prothi        3.955729 0.1087187 Estimable
## 4  ProTe        3.978682 0.1079482 Estimable
## 5   Metc        3.984402 0.1048774 Estimable
## 6    Chk        3.535239 0.1116943 Estimable

Comparing Model R1 though Model R5

The table below compares the five random-effects network meta-analysis models using AIC, BIC, and log-likelihood. All models share the same fixed effects structure (yield ~ trt), allowing valid comparison via AIC.

mods.asr = list(mod.r1,mod.r2,mod.r3,mod.r4,mod.r5)
asremlPlus::infoCriteria(mods.asr)

##   fixedDF varDF NBound       AIC       BIC   loglik
## 1       0     2      1 -414.6802 -406.0531 209.3401
## 2       0     7      1 -414.8112 -384.6163 214.4056
## 3       0    21      1 -457.8437 -367.2592 249.9219
## 4       0    11      2 -431.6604 -384.2114 226.8302
## 5       0    16      3 -460.6784 -391.6616 246.3392

Model R5 (Second-Order Factor Analytic) achieved the lowest AIC among all models evaluated, indicating the best overall fit. While estimating fewer parameters than the fully unstructured model (R3), R5 offers comparable or superior log-likelihood values, reflecting improved parsimony without sacrificing fit. Note that the AIC and log-likelihood values differ slightly from those reported in the original manuscript—likely because their values were computed using maximum likelihood, whereas the results here are based on REML. Nonetheless, both approaches consistently identify Model R5 as the best-fitting random effects model.

Final remarks

This post explored a series of increasingly flexible NMA models for multi-treatment trial data using ASReml-R. Starting from fixed-effects models with homogeneous variances (F1), we introduced separate variance components for each treatment (F2), and then expanded to random-effects models (R1–R5) incorporating structured variance-covariance matrices.

The compound symmetry (R1) and heterogeneous compound symmetry (R2) models provide useful baseline structures, while the unstructured model (R3) offers the most flexible fit—though at the cost of a large number of parameters. The factor analytic models (R4 and R5) strike a balance, efficiently capturing heterogeneity with fewer parameters. Notably, Model R5 (FA2) provided the best overall fit (lowest AIC), highlighting the value of using latent factors to explain treatment-by-trial interactions in networked agronomic data.

This framework is may be used in agricultural research where treatment replication is uneven across locations, and where borrowing strength across a network of trials improves inference. I believe other R packages, primarily open-source, can also be used like metafor, nlme, sommer, and I will try them in another post. All models here were based on summary-level data, which mirrors what’s often available from published field trials in plant pathology. In a future post, we will extend these methods to individual plot-level data (IPD). This opens multiple doors yet not heavily explored in the field.

R Statistics Network Meta-analysis ASReml

Vini Garnica

Postdoctoral Scholar

My research interests include agronomy and plant pathology matter.